The First Portfolio Optimization Technology to Earn Multiple Patents
New Frontier specializes in developing and applying state-of-the-art technology for investment practice. We began with improving mean-variance optimization, which had been the standard portfolio optimization process for almost fifty years, and continue to innovate on an ongoing basis.
Our investment committee uses our technology to create proprietary investment products, providing continuous feedback to the technology team. Meanwhile, our research team delves into the intricacies of the financial world, often producing new features for our technology, new investment offers, and new insights to share with investors around the world.
Michaud Optimization™
Michaud Optimization addresses information uncertainty by producing multiple sets of statistically-equivalent risk-return estimates surrounding the original estimates. These estimates are then used to compute various efficient frontiers, each optimized for the many possible ways assets may perform.
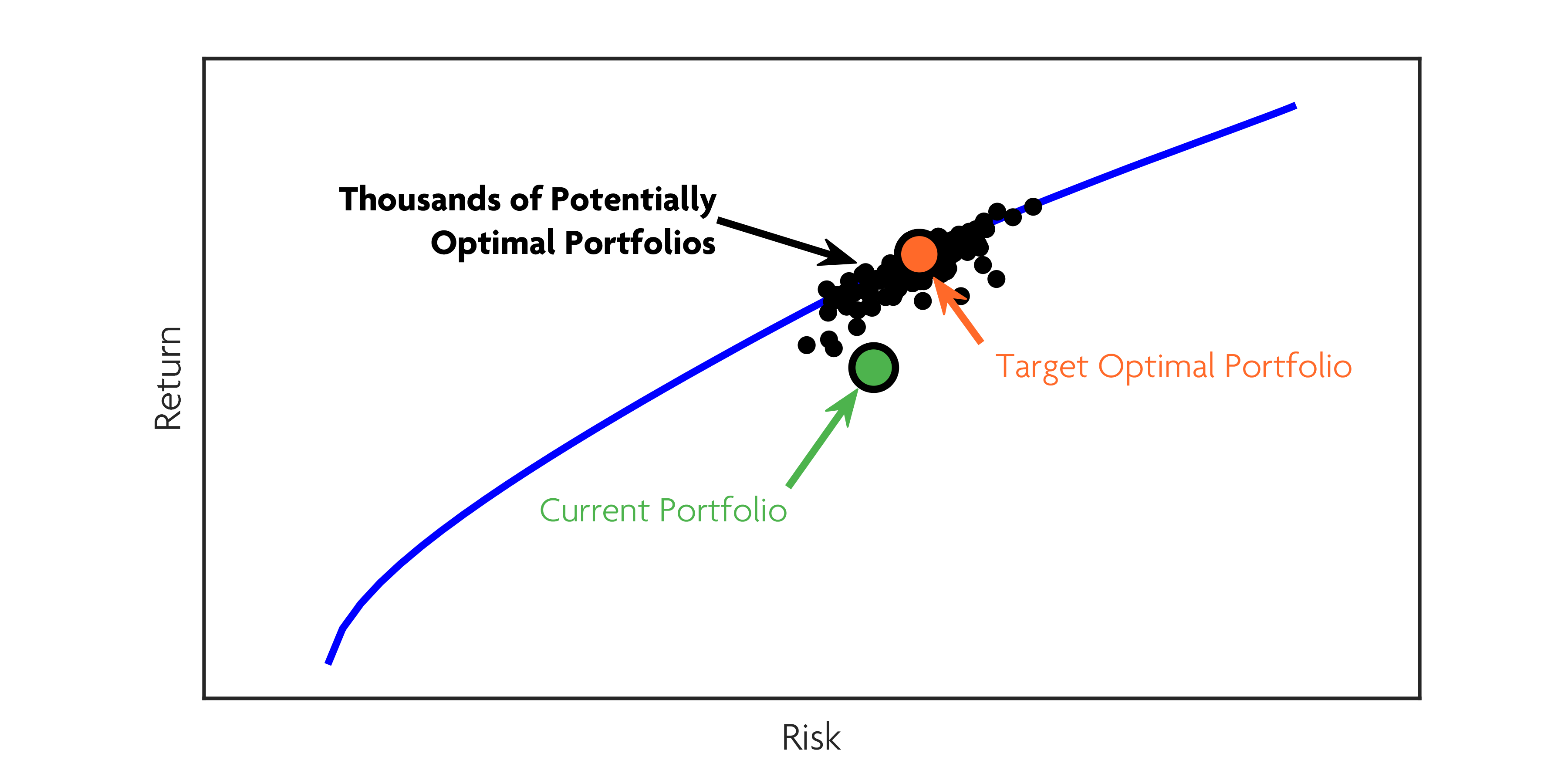
In traditional optimization, different datasets from the same underlying capital markets might produce a variety of different optimization inputs which in turn produce a variety of efficient frontiers, as pictured in this graph. Although they estimate the same market parameters and are therefore statistically equivalent, the differing input estimates produce a wide array of different optimized frontiers.
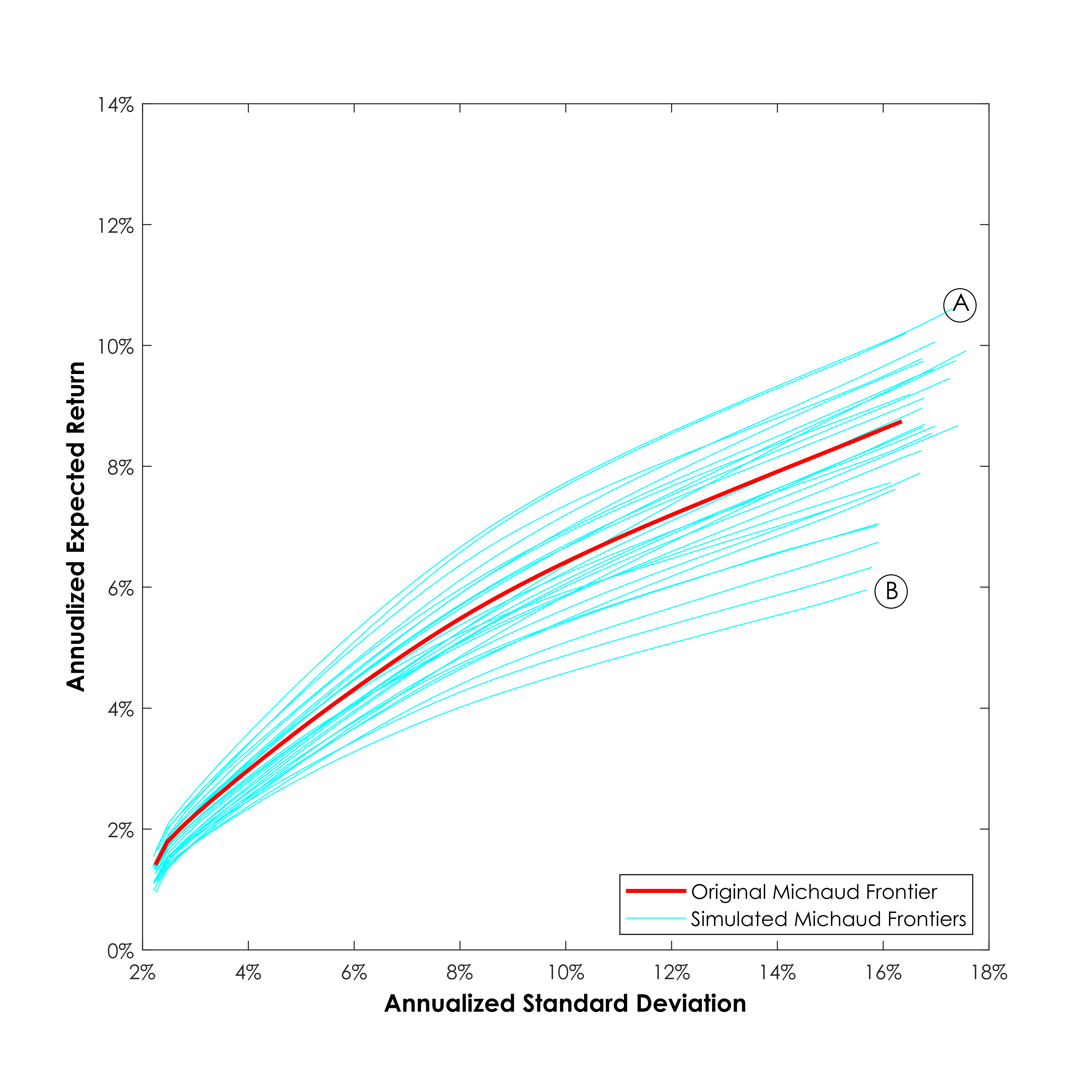
Because of this error-magnifying property of optimization, traditional efficient frontiers based on estimated assumptions could end up with very different outcomes, depending on the true data distribution and the errors in the estimates. An investor might think they are investing in portfolio “A” but actually be investing in portfolio “B.”
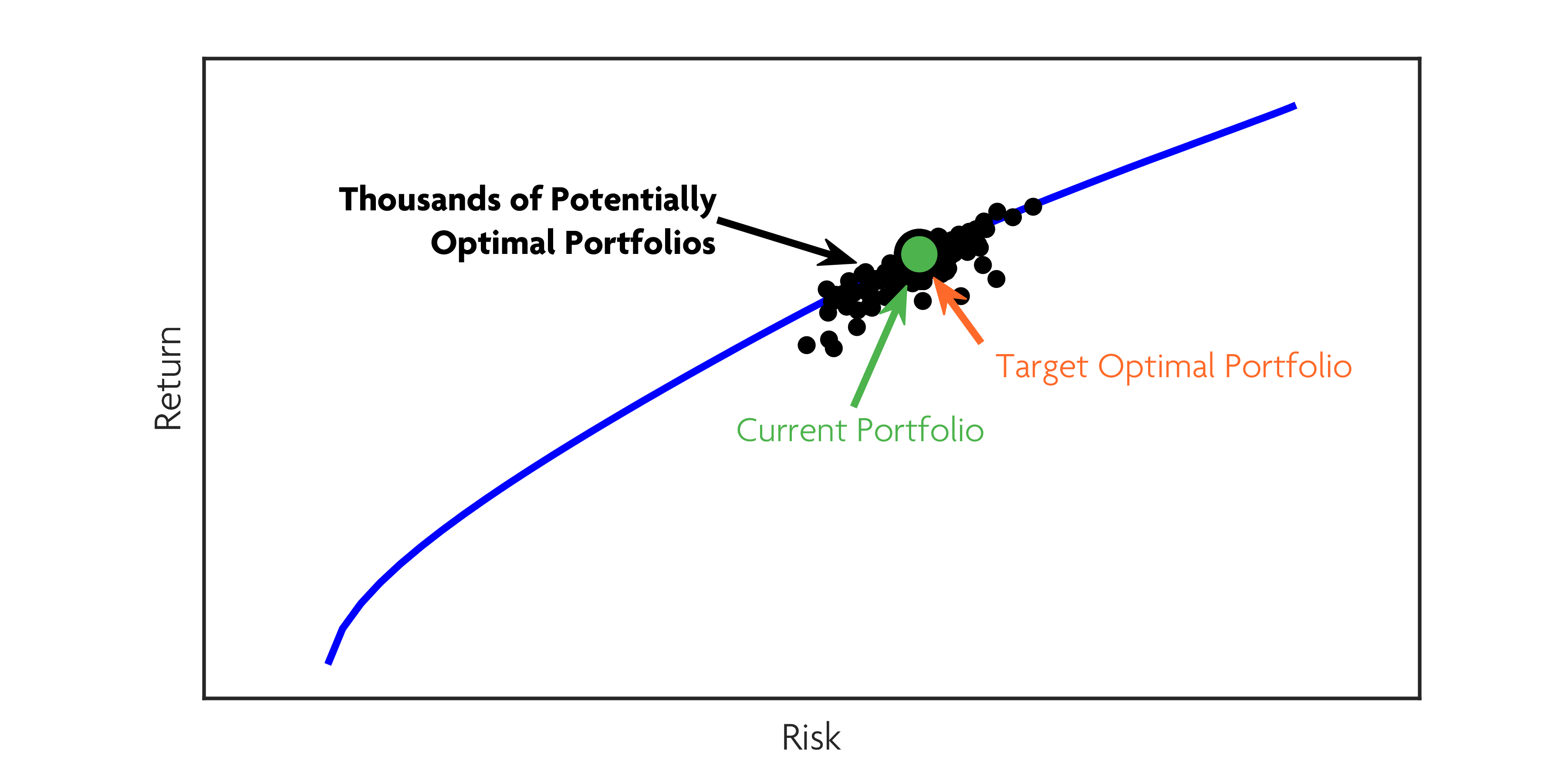
The Michaud optimization procedure simulates a set of possible inputs based on the error distribution, and includes them in the portfolio construction, properly accounting for all the possible errors in the dataset. Michaud frontiers based on a similar array of inputs produce more stable portfolios. The difference between “A” and “B”, while impossible to eliminate due to the variability of markets, is much less dramatic using Michaud Optimization.
Patented Rebalancing Test
Intelligent RebalancingTM
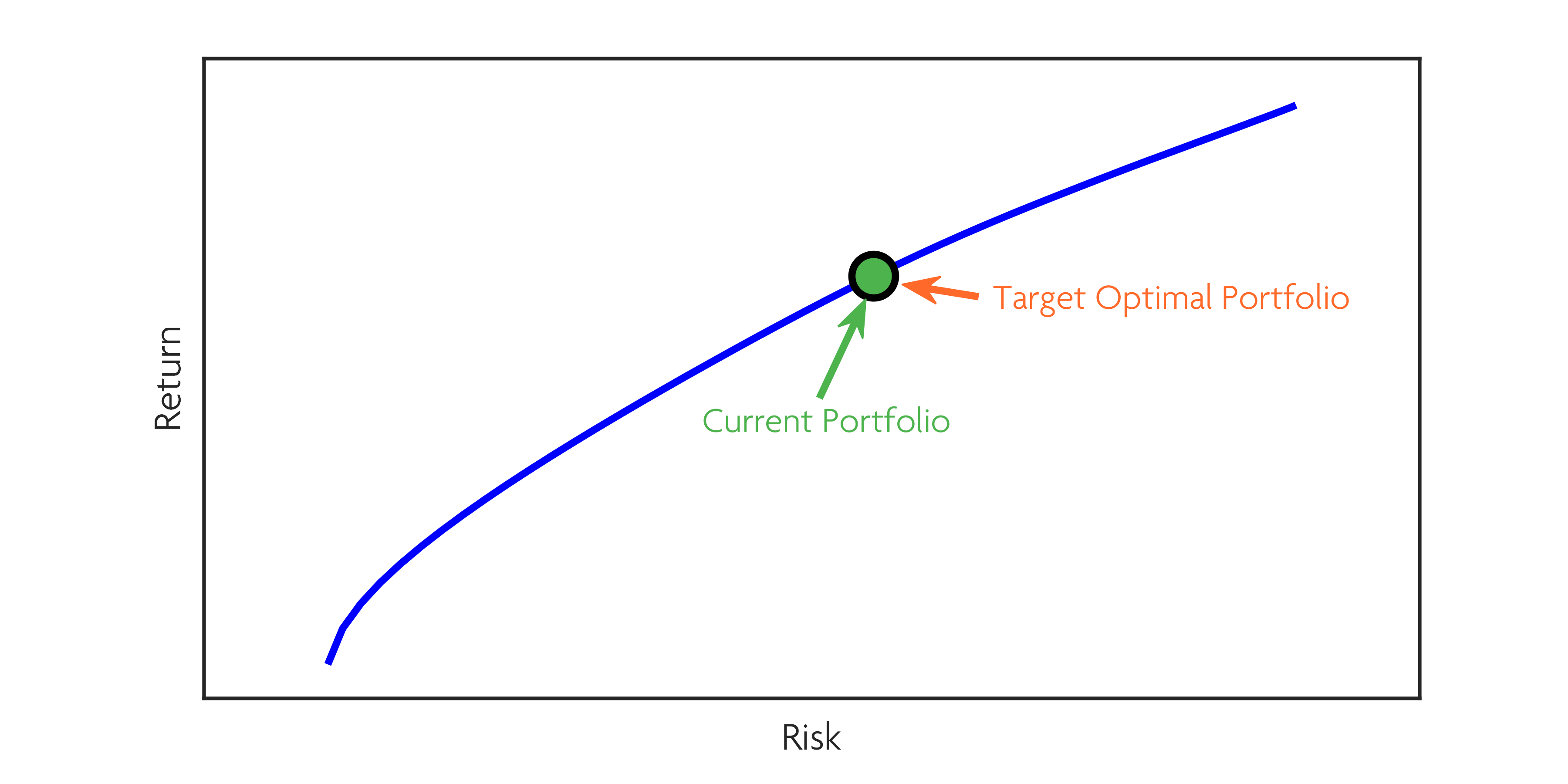
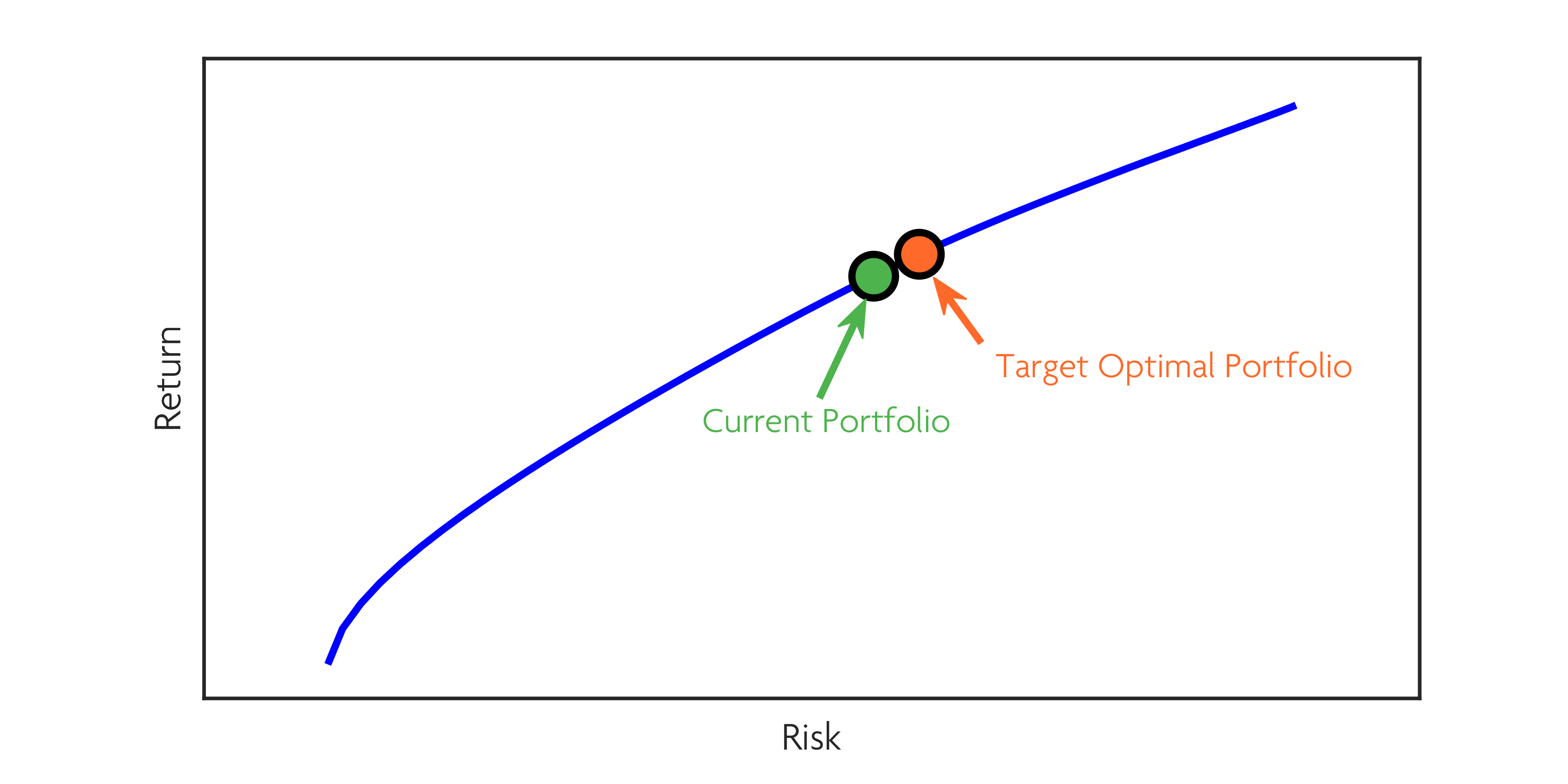
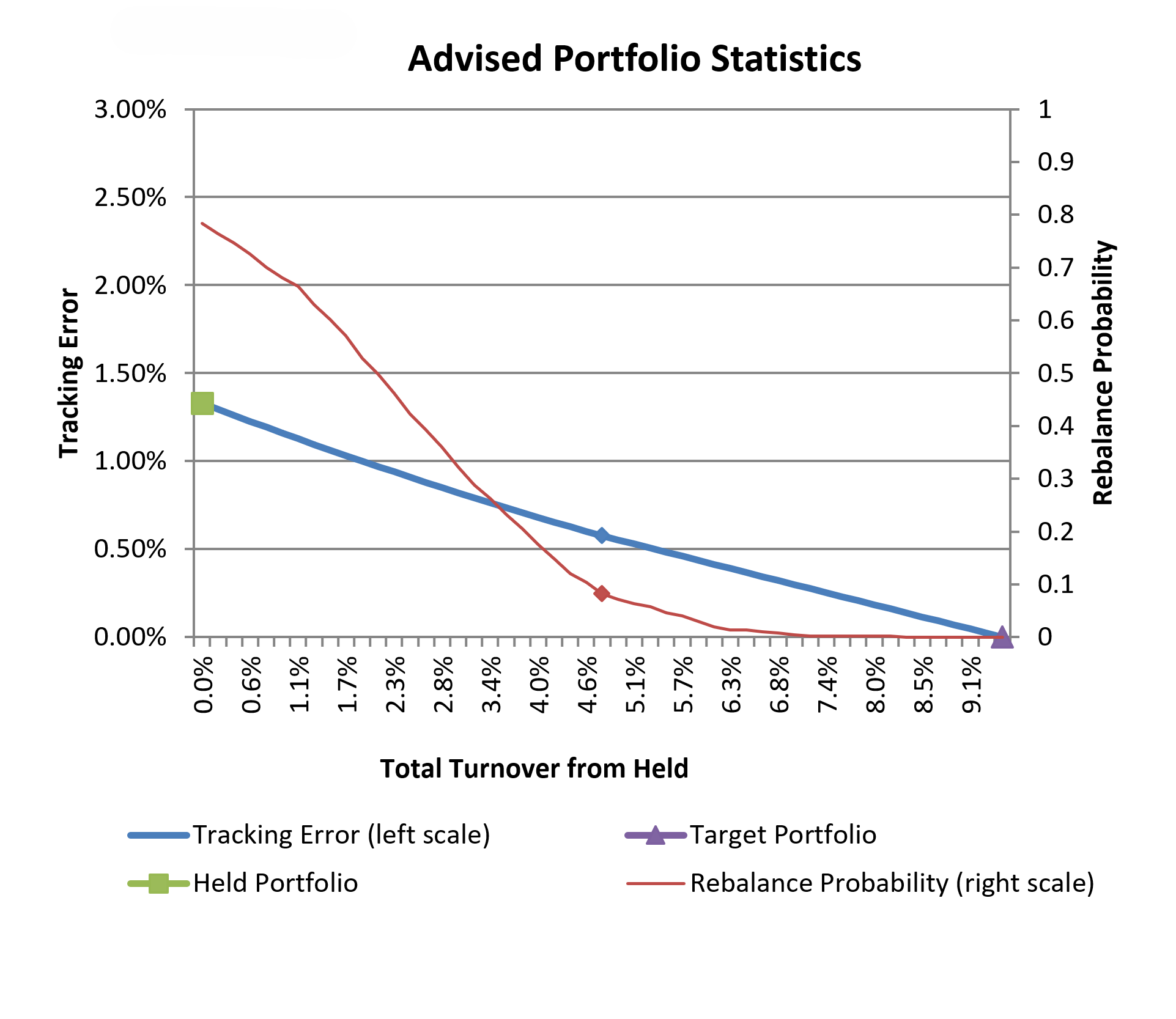
Michaud OptimizationTM provides the statistical framework for creating a rigorous procedure for portfolio rebalancing. Our patented rebalancing test determines whether or not a significant difference exists between the selected portfolio on the efficient frontier and the current holdings.
This need-to-trade test prevents ineffective and costly trades while enhancing investment value.
Trade Advisor
When our Portfolio Rebalancing test signals that it’s time to trade the portfolio, our proprietary Trade Advisor provides guidance on how to make the most effective partial trades. Trading may be costly or restricted due to tax considerations, and in these cases the Trade Advisor can find the optimal restricted trade to a statistically optimal portfolio, working around restrictions.
The technology is designed to identify the trading path with the least turnover or trading cost while minimizing tracking error and rebalance test score, satisfying any restrictions or constraints. It can also be paired with our post-optimize algorithm to eliminate small trades.
The Trade Advisor is the perfect companion to the Michaud OptimizerTM and Portfolio Rebalancing tools. Together, they form a complete system for creating the best model portfolios and tracking them efficiently with real-time investments.
Forecast Confidence
New Frontier’s Forecast Confidence works in concert with our Michaud Optimization and Rebalancing technologies. Forecast Confidence allows investors to tailor their optimization to their confidence in their estimates. With a lower forecast confidence setting, the optimizer will produce a more diversified portfolio to hedge against possible errors in the inputs, while higher forecast confidence will concentrate more into the assets with better input statistics.
This means that your portfolio will be optimally positioned for the likely range of outcomes based on your inputs and forecasts.
Discover More
Connect With Us
Learn more about how we work with financial advisors and institutions to deliver client-focused outcomes.